
ERATÓSTENES E A CIRCUNFERÊNCIA DA TERRA
No século 3 a.C., viveu em Alexandria, no Egito, um homem chamado Eratóstenes. Ele foi astrônomo, geógrafo, historiador, filósofo, poeta, crítico literário e matemático. Ele também foi diretor da famosa biblioteca de Alexandria.
Certa vez, ao folhear um livro da biblioteca, se deparou com um papiro que continha uma informação que lhe chamou atenção. Nele era dito que no dia mais longo do ano, em 21 de junho, à medida que o meio-dia se aproximava, as sombras das colunas do templo da cidade de Siena iam diminuindo até que não projetavam sombra nenhuma no chão, pois o sol ficava à pino, de maneira perpendicular. Por essa mesma razão, era possível ver o reflexo do sol no espelho d´água de certo poço da cidade. Essa descrição não chamaria a atenção da maioria das pessoas. No entanto, por ser um astrônomo perspicaz, Eratóstenes se lembrou que durante o solstício de 21 de junho qualquer coluna na cidade de Alexandria projetaria uma considerável sombra no chão. Por que em Siena isso não aconteceria? Seria falso o relato do papiro?
Projeção das sombras em Siena:


Se a Terra fosse plana, conforme se achava então, as sombras projetadas nas duas cidades deveriam ser exatamente as mesmas. Mas supondo que a informação do papiro era correta, Eratóstenes chegou à única conclusão lógica possível: a terra não é plana, e sim esférica!
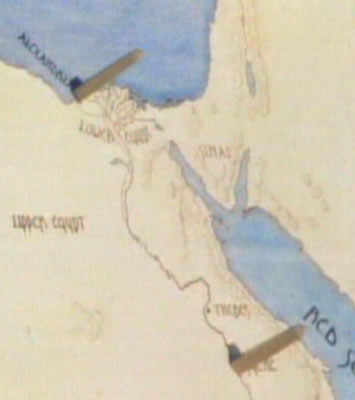
Modelo
plano: projeções iguais
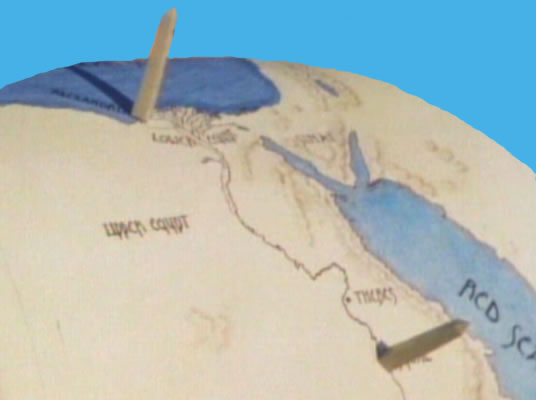
Modelo
esférico: projeções de sombra diferentes
Para testar sua teoria, Eratóstenes quis saber a distância exata entre Siena e Alexandria, para que pudesse calcular a circunferência da Terra, mediante um cálculo envolvendo ângulos e uma regra de três simples. Para tanto, contratou uma pessoa para contar os passos entre as duas cidades. A distância descoberta foi de 800 km. Diz uma lenda que o encarregado dessa tarefa gastou todo o solado das sandálias para cobrir esse grande percurso, o qual corresponde a 7 graus da curvatura da Terra, que tem um total de 360º. Para descobrir esses 7 graus bastava fincar uma vareta no chão e medir o ângulo da sombra projetada no chão, a qual, pela regra dos ângulos alternos internos, seria o mesmo ângulo formado pelos dois referenciais prolongados até o centro da Terra. Se uma outra cidade mais distante que não fosse Alexandria fosse escolhida para tal experimento, o ângulo da sombra aumentaria à medida que a distância fosse aumentando, tendo como referência a cidade de Siena. Isso pode ser percebido facilmente no diagrama abaixo. Imagine a vareta (objeto) descendo no círculo para a direita e os ângulos "A" e "B" aumentando em função desse deslocamento.
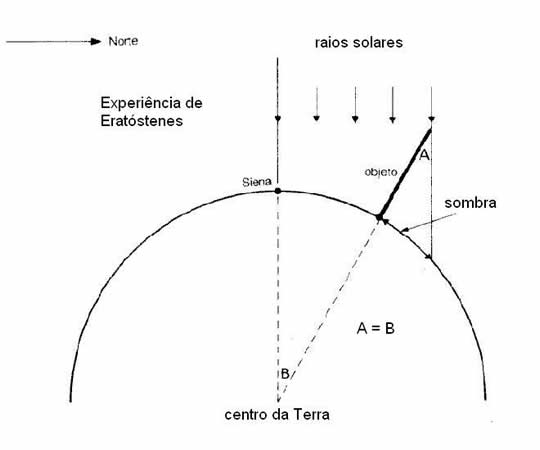
De posse dos dados que precisava, Eratóstenes fez um cálculo semelhante a este:
7 graus ------------ 800 Km
360 graus ------------ X
X = 41.142 Km
Eratóstenes descobriu não só que a Terra é redonda, mas demonstrou com pequena margem de erro o tamanho de sua circunferência. Conseguiu isso usando meramente sua inteligência atenta e algumas informações colhidas de maneira empírica. Note que tal descoberta se deu muitas centenas de anos antes das Idades Média e Moderna, quando a discussão sobre a esfericidade terrestre voltou à tona.

Se o conhecimento alcançado por sábios da antiguidade, a exemplo de Eratóstenes, não tivesse se perdido por causa da brutalidade dos homens de senso comum em suas guerras de conquistas, talvez vivêssemos hoje no "século 25"...
Fonte consultada:
"Cosmos", de Carl Sagan, episódio "As Margens do Oceano Cósmico".
Créditos das imagens, respectivamente:
1 - "Cosmos", de Carl Sagan, episódio "As Margens do Oceano Cósmico".
2 - Diagrama com ângulos alternos internos (adaptado)